Let’s Animate a SPIKE Robot Chicken with synchronized motors in Python! 🐔

Have you ever wanted to make a robot chicken that can walk and peck like a real one? Well, today you’re going to learn how a few lines of Python code can turn motors into a living, moving chicken! We’re using a cool robotics system called Pybricks, which works with LEGO® Powered Up motors and the Spike Prime Hub (basically a smart LEGO brain!).

Building a Chicken

For this tutorial, I built a robot chicken that can move each leg separately, with SPIKE Prime and the SPIKE expansion kit. It can also bend the neck and swivel its body from side to side. The body moves, so the chicken can put its weight on her standing leg, while swinging her free leg forward. The results in a walking motion. That is, if the motors are in the right positions relative to each other. This blog is about moving four motors at the same time and ensuring they are always in the right position compared to each other.

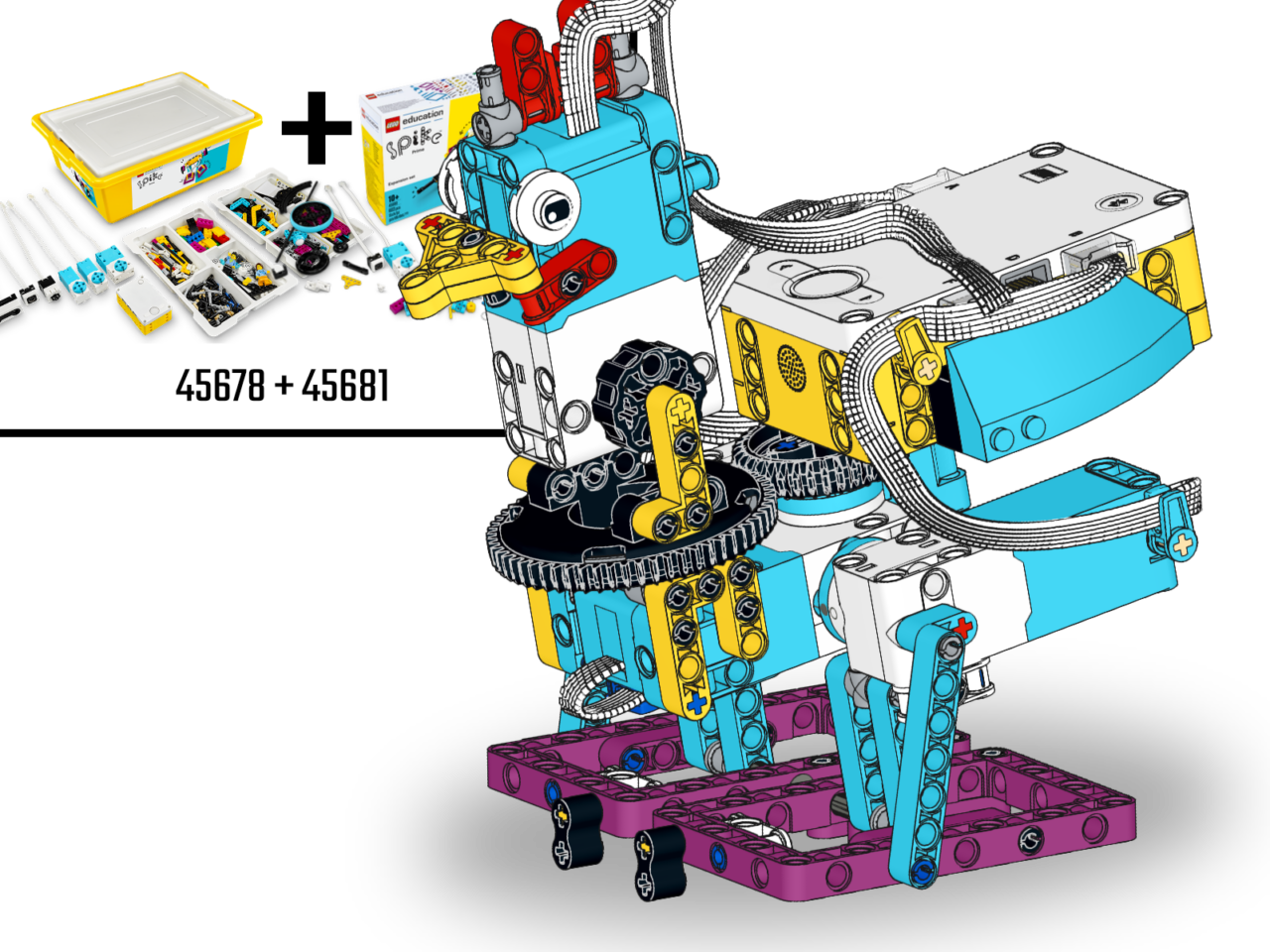
SPIKE Chicken

€7.50

Shop now

🤖 The SPIKE Chicken’s Body Parts

Just like a real chicken, our robot chicken has:

• A head (motor on Port F)
• A body (motor on Port E)
• Two legs (left leg on Port B, right leg on Port A)

These motors make the robot move! The code tells each part when and how much to move.

head = Motor(Port.F)
body = Motor(Port.E)
l_leg = Motor(Port.B)
r_leg = Motor(Port.A)

⏱ What is Animation with Keyframes?

Have you seen a flipbook where each page shows a drawing that’s just a little different? When you flip it fast, it looks like it’s moving. That’s animation! 🎬

We do something similar here using keyframes.

Each keyframe tells the motor:

• “At this time, be at this angle.”

For example:

head_walk = linear_interpolation([[0,0],[1000,0],[1100,-40],[2000,0]])

This means:

• At time 0ms: head is at angle 0
• At 1100ms: move to -40 (a little head bob)
• By 2000ms: back to 0

And what is linear interpolation anyway? Why is it needed in keyframe animation?

The magic of linear interpolation smoothly fills in the motion between keyframes. So instead of jumping from one to the next, it glides. To understand it, imagine you’re watching a cartoon or playing a video game.

Let’s say you know a character is standing on the left side of the screen at the start (like time = 0 seconds).

Then, 1 second later (time = 1 second), you know the character is way over on the right side of the screen.

But what about halfway through, at half a second (time = 0.5 seconds)? Where should the character be? The computer needs to figure that out to make the movement look smooth!

Linear Interpolation is just a fancy name for the simplest way to guess: Draw a straight line between the two spots you know, and find the point on that line.

Think of it like this:

1. You know Point A: (Time = 0s, Position = Left Side)
2. You know Point B: (Time = 1s, Position = Right Side)
3. You want to find Point C: (Time = 0.5s, Position = ???)

Linear interpolation says: “Okay, 0.5 seconds is exactly halfway between 0 seconds and 1 second. So, let’s put the character exactly halfway along a straight path between the Left Side and the Right Side.”

It’s like playing connect-the-dots, but only having two dots and drawing a single straight line between them. Then you look anywhere along that line to figure out where something should be.

A simple illustration of interpolation

Imagine a graph. The bottom line (X-axis) is Time. The side line (Y-axis) is the Position of the character (Left to Right). Draw it for yourself!

• We knew Point A (Start time, Left position).
• We knew Point B (End time, Right position).
• We drew a straight line (the / line) connecting A and B.
• To find the position at 0.5s, we went up from “0.5s” on the Time axis until we hit the line, then looked across to see the Position. It landed right in the Middle!

Why is it useful?

Computers use this all the time for:

• Animation: Making characters move smoothly between poses (keyframes).
• Games: Figuring out where objects should be between game updates.
• Graphs: Estimating values on a chart between the points that are actually plotted.
• Colors: Slowly fading from one color to another (like red to yellow, you go through orange in the middle).

So, Linear Interpolation is just a simple way to make a good guess for values that fall between other values you already know, by assuming things change steadily in a straight line. Linear interpolation is done with a bit of math, too detailed for this blog. I created some code you can easily import into your project, so you don’t have to do the math stuff. You can download the code at the end of this blog.

🐾 Walking Animation for a SPIKE chicken

The walk_anim uses keyframes for:

• The head (bobbing),
• The body (bouncing),
• The legs (stepping one at a time)

This makes our robot chicken strut like a boss!

walk_anim = Mechanism(
    motors, 
    [head_walk, body_walk, l_leg_walk, r_leg_walk]
)

And then we use this function to make the chicken walk. The animation needs to know what time it is to set the motors in the correct position. That’s why we pass it w.time(). That is the time on our stopwatch.

def walk(for_ms=5000):
    w = StopWatch()
    while w.time() < for_ms:
        walk_anim.update_motor_pwms(w.time())
    walk_anim.stop()

🪿 Animate the SPIKE chicken for Pecking

You know how chickens poke the ground looking for food? That’s called pecking! 🐤

We made a peck animation by moving just the head and body:

head_peck = linear_interpolation([(0,-30),(300,-90),(1000,-30)])
body_peck = linear_interpolation([(0,-20),(300,-20),(1000, 20),(1300,20),(2000, -20)])

This makes the chicken duck its head down, then pop back up. Since the head is connected to the body, it will look a bit left and right, because the body also bobs left and right. Next we create the animation by building a Mechanism that contains the motors and their keyframes.

peck_anim = Mechanism([head, body], [head_peck, body_peck])

And here’s the pecking function:

def peck(for_ms=5000):
    # pre-peck leg motion
    r_leg.run_target(300,40,wait=False)
    l_leg.run_target(300,40,wait=True)

    # peck loop
    while w.time() < for_ms * 1.5:
        peck_anim.update_motor_pwms(w.time())
    
    # reset all parts
    head.run_target(300,0)
    r_leg.run_target(300,0)
    l_leg.run_target(300,0)

🎬 Putting the SPIKE chicken animation together

At the end of the program, we tell our chicken:

1. Walk for 7 seconds
2. Peck for 5 seconds
3. Walk again for 10 seconds

Since Pybricks counts time in miliseconds – that is a thousanth of a second –

walk(7000)
peck(5000)
walk(10000)

And just like that, you’ve got a lifelike robot chicken doing its thing! 🐥

Here is the full code, so you can read in one go. Remember that you need to download and import motor_sync.py into Pybricks to make use of my animation library.

from pybricks.hubs import PrimeHub
from pybricks.pupdevices import Motor
from pybricks.parameters import Direction, Port
from pybricks.tools import StopWatch
from motor_sync import Mechanism, linear_interpolation, AMHTimer

# Initialize the hub and motors
hub = PrimeHub()

head = Motor(Port.F)
body = Motor(Port.E)
l_leg = Motor(Port.B)
r_leg = Motor(Port.A, positive_direction=Direction.COUNTERCLOCKWISE)  # Reverse direction for proper movement

motors = [head, body, l_leg, r_leg]

# Define motion profiles using linear interpolation for a walking animation
head_walk = linear_interpolation([
    [0, 0],      # At time 0, be at position 0
    [1000, 0],   # Stay at 0 for 1000ms
    [1100, -40], # At time 1100ms be at position -40
    [2000, 0]    # End at position 0, the same as the start position. Repeat.
])

body_walk = linear_interpolation([
    [0, -35], 
    [1000, 35], 
    [2000, 35], 
    [3000, -35], 
    [4000, -35]
])

l_leg_walk = linear_interpolation([
    [0, -10], 
    [1000, 40], 
    [2000, -10], 
    [3000, -10], 
    [4000, -10]
])

r_leg_walk = linear_interpolation([
    [0, -10], 
    [1000, -10], 
    [2000, -10], 
    [3000, 40], 
    [4000, -10]
])

# Create walking animation mechanism
walk_anim = Mechanism(
    motors, 
    [head_walk, body_walk, l_leg_walk, r_leg_walk]
)

# Define motion profiles for pecking animation
head_peck = linear_interpolation([
    (0, -30), 
    (300, -90), 
    (1000, -30)
])

body_peck = linear_interpolation([
    (0, -20), 
    (300, -20), 
    (1000, 20), 
    (1300, 20), 
    (2000, -20)
])

# Create pecking animation mechanism
peck_anim = Mechanism(
    [head, body], 
    [head_peck, body_peck]
)

# Function to perform walking animation
def walk(for_ms=5000):
    w = StopWatch()
    while w.time() < for_ms:
        walk_anim.update_motor_pwms(w.time())
    walk_anim.stop()

# Function to perform pecking animation
def peck(for_ms=5000):
    speed_up = 1.5
    w = AMHTimer(rate=1000 * speed_up)  # Faster timer for animation speed-up

    # Reset body and legs to initial positions
    body.run_target(300, 0)
    r_leg.run_target(300, 40, wait=False)
    l_leg.run_target(300, 40, wait=True)

    # Play pecking animation
    while w.time() < for_ms * speed_up:
        peck_anim.update_motor_pwms(w.time())
    peck_anim.stop()

    # Return motors to neutral positions
    head.run_target(300, 0, wait=False)
    r_leg.run_target(300, 0, wait=False)
    l_leg.run_target(300, 0, wait=True)

# Demo sequence
walk(7000)
peck(5000)
walk(10000)

🚀 What You Learned about animating a SPIKE robot

• How to use motors to animate a robot
• What keyframes and interpolation are
• How to make walking and pecking animations
• How code + creativity = fun robotics projects!

So, are you ready to make your chicken dance the robot? 🤖🐔

Go ahead, tweak the code! Make it scratch the ground or even moonwalk. The sky’s the limit!

Here’s the motor_sync module:

• motor_sync.py

Have questions or want to show off your robot chicken? Drop a comment below! 👇